Many computer security systems rely on so-called RSA keys,
this is particularly the case in electronic commerce.
To summarize in a very simplified way, this is a code created from the multiplication of 2 large prime numbers
Here is an example:

Currently largest key
Mathematically
A prime number is a number that is not a product of two smaller numbers, except 1 and itself.
If the operation of multiplying 2 numbers immediately gives the product,
conversely,
it is almost impossible to find these 2 numbers from a single result .
Indeed, that would require to test all the combinations of multiplications of the lower prime numbers to find the correct one.
And the larger the result, the more calculations are required, which could require the use of hundreds of computers, working together and for years.
In other words, computer security relies on the fact that
it is physically impossible to break code in a reasonable amount of time.
But this protection is completely questioned if one uses quantum computers, and more precisely by implementing the Shor's algorithm.
This algorithm was developed by Peter Shor in 1994.
Rather than directly looking for the 2 prime factors of a number N, Shor suggests doing it differently.
It goes through an intermediate function which offers the possibility of using the superimposed states of the qubits,
as well as rotation operations on the results, so that the values to be rejected are excluded
and those that give the solution amplify their probability of being measured.
In the end, what would have taken several years on classical computers will only take a few seconds on a quantum computer with enough of qubits.
We propose a tool that allows you to visualize the intermediate states of the qubits during the algorithm.
Remember that in nature, it is impossible to follow the intermediate states to debug
since the physical observation destroys the superimposed states.
Thanks to our visualization tools, this constraint can be overcome.
Let yourself be guided after clicking on the "launch the experience" button below.
First, you can leave the default values and click OK
Then click as many times as necessary on the measure checkbox to obtain the answer in green panel.
It is not necessary to understand what is going on at this point: just observe the states of the qubits by hovering your cursor over the graphical elements.
Warning: the tool is not really suitable for reading on a smartphone
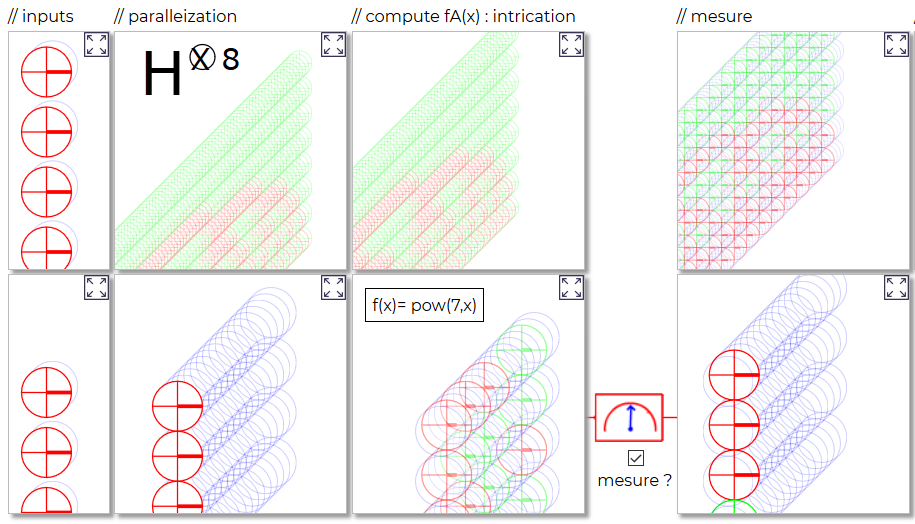
Above part of the experiment screen
Some precisions
Shor's algorithm is divided into 2 parts:
- a classical calculation of gcd (greatest common divisor) between our number N and a random number A
- a quantum computation which searches for the period of the function A
x .
Quantum computing uses what is called a
quantum fourier transform.
Mathematically
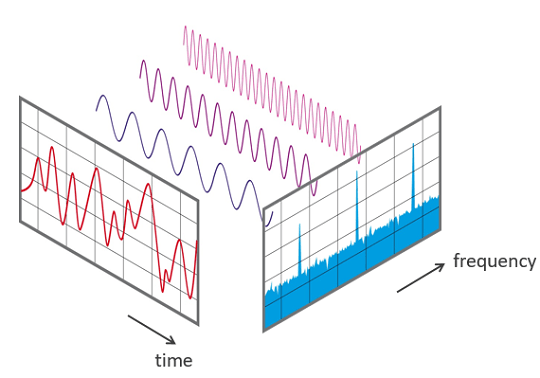
A classical Fourier transform makes it possible to analyze a complex signal by decomposing it into frequencies.
A quantum Fourier transform generalizes this principle to all qubit states and their probability
of being measured.
Interlude: Let's have fun with the fourier transform.
By drawing on the surface above, your line is automatically decomposed into sine waves, thanks to a fourier transform.
But this time, each wave is not represented as a peak at a certain frequency, nor as a horizontal sine wave,
but like the path of a point circulating on a circle with a certain speed.
Back on topic
Here is how the literature on the subject represents Shor's algorithm in the form of circuits.
Our tool available in the interactive experience deviates from it since we focus on showing the states of the qubits, rather than the wiring of the elements:
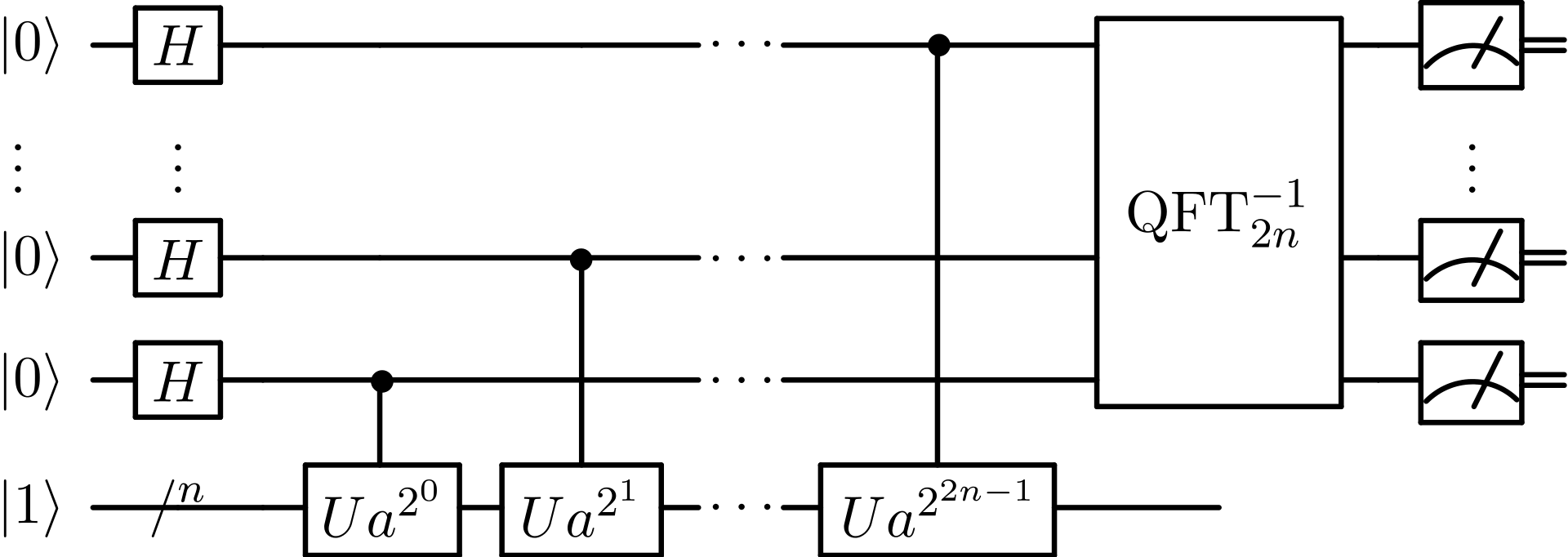
Implementation circuit