Beaucoup de systèmes de sécurité informatique reposent sur ce qu’on appelle des clés RSA,
c’est notamment le cas dans le commerce électronique.
Pour résumer de façon très simplifiée, il s’agit d’un code créé à partir de la multiplication de 2 grands nombres premiers
En voici un exemple :

Clé la plus grande actuellement
Sur le plan mathématique
Un nombre premier est un nombre qui n’est pas divisible par un autre nombre, sauf lui-même et 1.
Si l’opération qui consiste à multiplier 2 nombres donne le produit immédiatement,
inversement,
il est quasiment impossible de retrouver ces 2 nombres à partir du seul résultat.
En effet, cela demanderait de tester toutes les combinaisons de multiplications des nombres premiers inférieurs pour trouver la bonne.
Et plus le résultat est grand, plus il faut de calculs, lesquels pourraient nécessiter d’utiliser des centaines d’ordinateurs, travaillant conjointement et durant des années.
Autrement dit, la sécurité informatique repose sur le fait qu’
il est physiquement impossible de casser le code en un temps raisonnable.
Mais cette protection est complètement remise en question si on utilise des ordinateurs quantiques, et plus précisément en implémentant l’algorithme de Shor.
Cet algorithme a été élaboré par Peter Shor en 1994.
Plutôt que de rechercher directement les 2 facteurs premiers d’un nombre N, Shor propose de procéder différemment.
Il passe par une fonction intermédiaire qui offre la possibilité d’utiliser les superpositions d’états des qubits,
ainsi que des opérations de rotation sur les résultats, de telle sorte que les valeurs à rejeter s’excluent
et que celles qui donnent la solution amplifient leur probabilité d’être mesurées.
Au final ce qui aurait pris plusieurs années sur des ordinateurs classiques ne prendra que quelques secondes sur un ordinateur quantique disposant de suffisamment de qubits.
Nous vous proposons un outil qui permet de visualiser les états intermédiaires des qubits durant l'algorithme.
On rappelle que dans la nature, il est impossible de suivre les états intermédiaires pour deboguer puisque la lecture physique détruit les états superposés.
Grâce à nos outils de visualisation, cette contrainte peut être dépassée.
Laissez-vous guider après avoir cliqué sur le bouton "lancer l'expérience" ci-dessous.
Dans un premier temps, vous pouvez laisser les valeurs par défaut et cliquer sur OK
Puis cliquez autant de fois que nécessaire sur la case à cocher "mesure" pour obtenir la réponse en vert.
Ce n'est pas nécessaire de comprendre ce qui se passe à ce stade : observez juste les états des qubits en passant votre curseur sur les éléments graphiques.
Attention : l'outil n'est pas adapté à la lecture sur smartphone
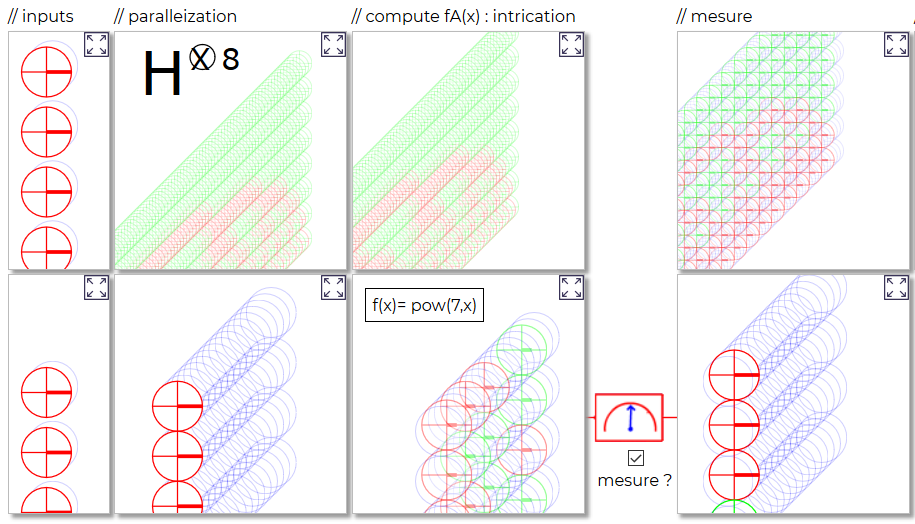
Ci-dessus une partie de l'écran de l'expérience
Quelques précisions
L'algorithme de Shor est divisé en 2 parties :
- un calcul classique de pgcd (plus grand commun diviseur) entre notre nombre N et un nombre A aléatoire
- un calcul quantique qui cherche la période de la fonction A
x.
Le calcul quantique utilise ce qui s'appelle une
transformée de fourier quantique.
Sur le plan mathématique
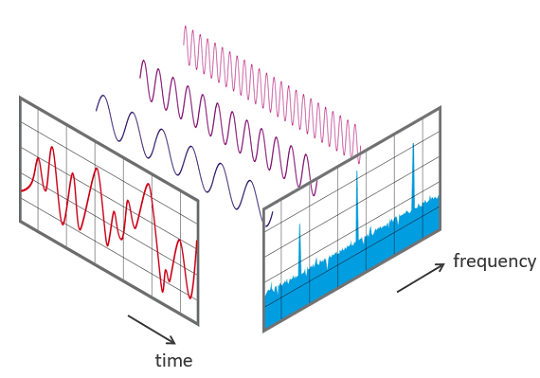
Une transformée de Fourier classique permet d'analyser un signal complexe en le décomposant en fréquences.
Une transformée de Fourier quantique généralise ce principe à tous les états des qubits et à leur probabilité d'être mesurés.
Intermède : Amusons-nous avec la transformée de fourier
En dessinant dans la surface ci-dessus, votre trait est automatiquement décomposé en ondes sinusoidales, grâce à une transformée de fourier.
Mais cette fois, les ondes ne sont pas représentées comme des pics à une certaine fréquence, ni comme des sinusoides horizontales,
mais comme le chemin d'un point circulant sur un cercle avec une certaine vitesse.
Revenons à nos moutons
Voici comment la littérature sur le sujet représente l'algorithme de Shor sous forme de circuits.
Notre outil disponible dans l'expérience interactive s'en écarte puisque nous nous attachons à montrer les états des qubits, plutôt que le câblage des éléments :
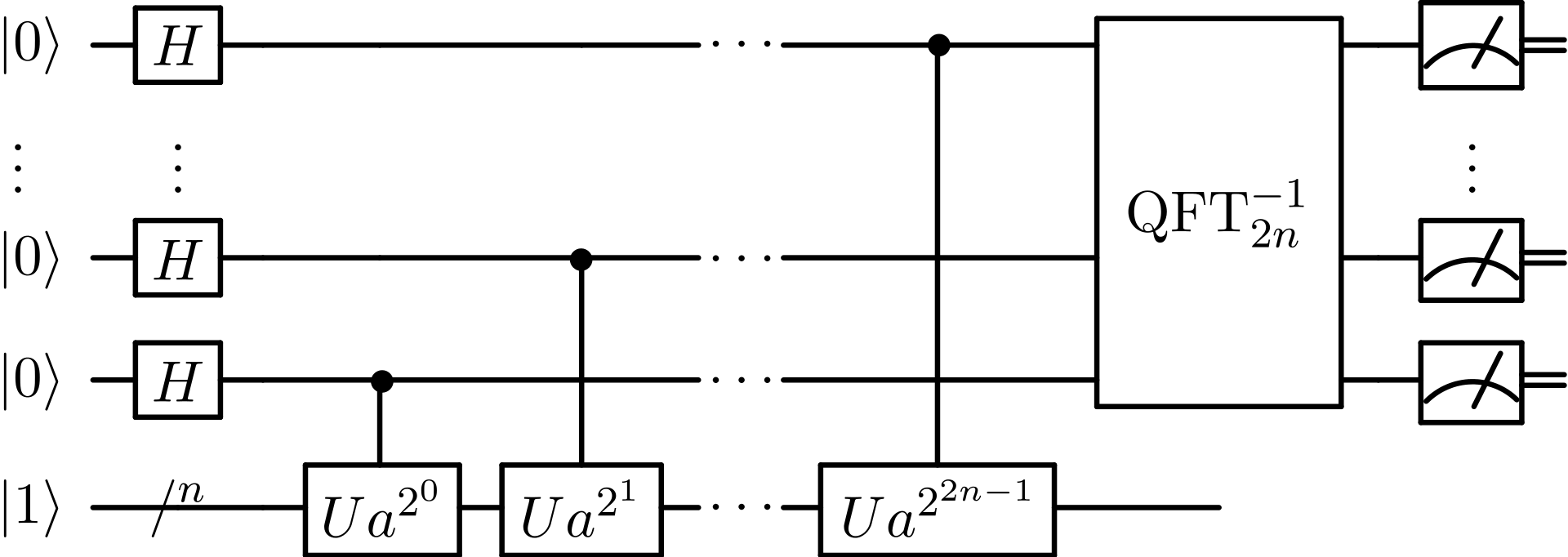
Circuit d'implémentation